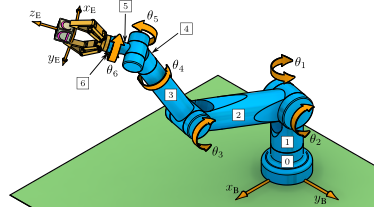
Robot Mechanics and Control Robot Mechanics and Control

Example 5.07:: Offset Articulate Manipulator: Jacobian Computation (MATLAB)

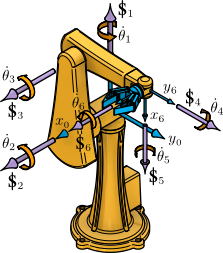
RP Polar Manipulator

This example illustrates a computation with specific joint values for the offset articulate manipulator Jacobian. See textbook example description for an interpretation of the screw coordinates.

Contents

Clear All Workspace Objects and Reset All Assumptions

%clear all

Structural Parameters

a2 = 43; % cm
d3 = 18; % cm
d4 = 43; % cm

Joint Values

theta1 = 90; % deg
theta2 = 90; % deg
theta3 = -180; % deg
theta23 = theta2 + theta3; % deg
theta4 = 90; % deg
theta5 = 90; % deg
theta6 = -90; % deg

Local Variables From U-Matrices

U511 = cosd(theta5)*cosd(theta6);
U512 = -cosd(theta5)*sind(theta6);
U521 = sind(theta5)*cosd(theta6);
U522 = -sind(theta5)*sind(theta6);

U411 = -sind(theta4)*sind(theta6) + U511*cosd(theta4);
U412 = -sind(theta4)*cosd(theta6) + U512*cosd(theta4);
U413 = -cosd(theta4)*sind(theta5);
U421 = cosd(theta4)*sind(theta6) + U511*sind(theta4);
U422 = cosd(theta4)*cosd(theta6) + U512*sind(theta4);
U423 = -sind(theta4)*sind(theta5);

U311 = U411*cosd(theta3) - U521*sind(theta3);
U312 = U412*cosd(theta3) - U522*sind(theta3);
U313 = -sind(theta3)*cosd(theta5) + U413*cosd(theta3);
U314 = -d4*sind(theta3);
U321 = U411*sind(theta3) + U521*cosd(theta3);
U322 = U412*sind(theta3) + U522*cosd(theta3);
U323 = cosd(theta3)*cosd(theta5) + U413*sind(theta3);
U324 = d4*cosd(theta3);

U211 = U411*cosd(theta23) - U521*sind(theta23);
U212 = U412*cosd(theta23) - U522*sind(theta23);
U213 = -sind(theta23)*cosd(theta5) + U413*cosd(theta23);
U214 = a2* cosd(theta2) - d4*sind(theta23);
U221 = U411*sind(theta23) + U521*cosd(theta23);
U222 = U412*sind(theta23) + U522*cosd(theta23);
U223 = cosd(theta23)*cosd(theta5) + U413*sind(theta23);
U224 = a2*sind(theta2) + d4*cosd(theta23);

Joint-Screw 1: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{1|6}$

Jacobian(:,1) = [ U221; U222; U223; d3*U211 + U214*U421; d3*U212 + U214*U422; d3*U213 + U214*U423];

Joint-Screw 2: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{2|6}$

Jacobian(:,2) = [-U421; -U422; -U423; U214*U221 - U211*U224; U214*U222 - U212*U224; U214*U223 - U213*U224];

Joint-Screw 3: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{3|6}$

Jacobian(:,3) = [-U421; -U422; -U423; U314*U321 - U311*U324; U314*U322 - U312*U324; U314*U323 - U313*U324];

Joint-Screw 4: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{4|6}$

Jacobian(:,4) = [ U521; U522; cosd(theta5); 0; 0; 0];

Joint-Screw 5: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{5|6}$

Jacobian(:,5) = [ -sind(theta6); -cosd(theta6); 0; 0; 0; 0];

Joint-Screw 6: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{6|6}$

Jacobian(:,6) = [0; 0; 1; 0; 0; 0];

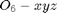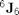
The Jacobian Resolved in $O_{6}-xyz$: $^{6}\mathbf{J}_{6}$

J6Res6 = Jacobian

J6Res6 =

    -1     0     0     0     1     0
     0     0     0     1     0     0
     0     1     1     0     0     1
     0   -43   -43     0     0     0
    18   -43     0     0     0     0
   -43     0     0     0     0     0

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.


Published with MATLAB® R2014a