Robot Mechanics and Control Robot Mechanics and Control

Example 5.06:: 2R Planar: Joint Rates, Example 2 (MATLAB)

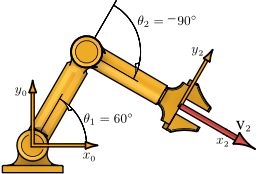
2R Planar Manipulator

This example uses the inverse Jacobian to compute the joint rates for the 2R planar manipulator. It uses the 2 $\times$ 2 Jacobian resolved in the end-effector frame.

Contents

Clear All Workspace Objects and Reset All Assumptions

clear all

Structural Parameters

a1 = 30; % cm
a2 = 30; % cm

Given Joint Values

theta1 = 60; % deg
theta2 = -90; % deg
theta12 = theta1 + theta2; % deg

End-effector Linear Velocity Resolved in 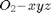$O_{2}{\mathrm -}xyz$

V2Res2 = [60; 0]; % [cm/s]

Inverse Jacobian: $[^{2}\overline\mathbf{J}_{2}]^{-1}$

detJ2Res2 = a1*a2*sind(theta2);
invJ2Res2 = (1/detJ2Res2)*[ a2,                      0;
                           -(a2 + a1*cosd(theta2)),  a1*sind(theta2)];

Joint Rates 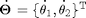$\dot{\mathbf \Theta} = \{ \dot{\theta}_{1}, \dot{\theta}_{2} \}^{\mathrm T}$ in rad/s

ThetaDot = invJ2Res2*V2Res2 % [rad/s]

ThetaDot =

    -2
     2

Joint Rates 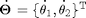$\dot{\mathbf \Theta} = \{ \dot{\theta}_{1}, \dot{\theta}_{2} \}^{\mathrm T}$ in deg/s

ThetaDotDeg = (180/pi)*ThetaDot % [deg/s]

ThetaDotDeg =

 -114.5916
  114.5916

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.


Published with MATLAB® R2014a