Robot Mechanics and Control Robot Mechanics and Control

Example 5.02:: Helical Pair: Screw Coordinates (MATLAB)

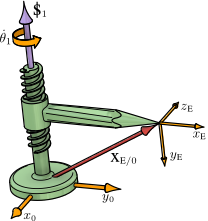
Helical Pair, Screw Coordinates

This example illustrates how to determine a helical pair's joint-rate, screw coordinates, and pitch from its Cartesian twist 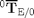$^{0}\overline{\mathbf T}_{{\mathrm E}/0}$.

Contents

Clear All Workspace Objects and Reset All Assumptions

%clear all

The Cartesian twist 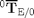$^{0}\overline{\mathbf T}_{{\mathrm E}/0}$

TwistERel0Res0 = [0; 0; 2; -40; 0; 10] % [rad/s; cm/s]

TwistERel0Res0 =

     0
     0
     2
   -40
     0
    10

a) The Joint-Rate 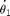$\dot{\theta}_{1}$

omegaERel0Res0 = [TwistERel0Res0(1); TwistERel0Res0(2); TwistERel0Res0(3)]; % [rad/s]
VERel0Res0 = [TwistERel0Res0(4); TwistERel0Res0(5); TwistERel0Res0(6)]; % [cm/s]
theta1Dot = norm(omegaERel0Res0) % rad/s

theta1Dot =

     2

b) Screw Coordinates $^{0}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{1|\mathrm E}$

S1Res0 = omegaERel0Res0/theta1Dot %[unitless]
SO1ERes0 = VERel0Res0/theta1Dot % [cm]
Screw1ERes0 = [S1Res0; SO1ERes0] % [unitless; cm]

S1Res0 =

     0
     0
     1


SO1ERes0 =

   -20
     0
     5


Screw1ERes0 =

     0
     0
     1
   -20
     0
     5

c) Pitch 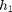$h_{1}$

h1 = dot(S1Res0, SO1ERes0) % cm

h1 =

     5

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.


Published with MATLAB® R2014a