
|
|
|
|
|
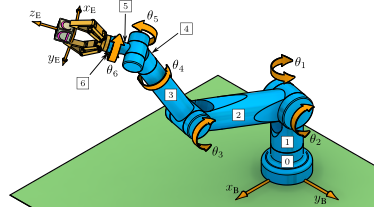
Example 4.07:: Offset Articulate Manipulator: Algebraic Solution (MATLAB)
This example uses the algebraic method to compute the inverse kinematics for the offset articulate manipulator. It uses the functions OffsetArticulateShoulder, OffsetArticulateElbow, and OffsetArticulateWrist to compute the eight sets of joint values. After computing the solutions, we check them by substituting the joint values into the forward kinematics transformation OffsetOffsetArticulateFK.
Contents
- Clear All Workspace Objects and Reset All Assumptions
- Structural Parameters
- Position and Orientation of
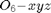
- Normal, Orientation, Approach, and Position Vectors
- Solution 1: Left-Shoulder, Elbow-Down, No-Flip
- Solution 2: Left-Shoulder, Elbow-Down, Flip
- Solution 3: Left-Shoulder, Elbow-Up, No-Flip
- Solution 4: Left-Shoulder, Elbow-Up, Flip
- Solution 5: Right-Shoulder, Elbow-Down, No-Flip
- Solution 6: Right-Shoulder, Elbow-Down, Flip
- Solution 7: Right-Shoulder, Elbow-Up, No-Flip
- Solution 8: Right-Shoulder, Elbow-Up, Flip
- Eight Manipulator Configurations with the Same End-Effector Position/Orientation
- Check the Solutions
Clear All Workspace Objects and Reset All Assumptions
clear all
Structural Parameters
a2 = 43; % cm d3 = 18; % cm d4 = 43; % cm
Position and Orientation of 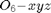
Given transformation 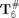
T6N = [ 0 0 1 18
0 1 0 43
-1 0 0 43
0 0 0 1 ];
Normal, Orientation, Approach, and Position Vectors
Extract these vectors from 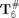
nx = T6N(1,1); ny = T6N(2,1); nz = T6N(3,1); ox = T6N(1,2); oy = T6N(2,2); oz = T6N(3,2); ax = T6N(1,3); ay = T6N(2,3); az = T6N(3,3); px = T6N(1,4); py = T6N(2,4); pz = T6N(3,4);
Solution 1: Left-Shoulder, Elbow-Down, No-Flip
% theta1: Left-Shoulder theta1L = atan2d(py, px) + atan2d(d3, -sqrt(px*px + py*py - d3*d3)); % deg [V112, V113, V114, V132, V133, f3] = OffsetArticulateShoulder(T6N, a2, d4, theta1L); % theta2, theta3: Elbow-Down theta2LD = atan2d(pz, V114) + atan2d(sqrt(V114*V114 + pz*pz - f3*f3), f3); % deg [V312, V313, V323, V332, V333, theta3LD] = OffsetArticulateElbow(T6N, a2, V112, V113, V114, V133, theta2LD); % theta4, theta5, thet6: No-Flip theta4LDNF = atan2d(-V323, -V313); % deg [theta5LDNF, theta6LDNF] = OffsetArticulateWrist(V132, V133, V312, V313, V332, V333, theta4LDNF);
Solution 2: Left-Shoulder, Elbow-Down, Flip
% theta4, theta5, theta6: Flip theta4LDF = atan2d(V323, V313); % deg [theta5LDF, theta6LDF] = OffsetArticulateWrist(V132, V133, V312, V313, V332, V333, theta4LDF);
Solution 3: Left-Shoulder, Elbow-Up, No-Flip
% theta2, theta3: Elbow-Up theta2LU = atan2d(pz, V114) + atan2d(-sqrt(V114*V114 + pz*pz - f3*f3), f3); % deg [V312, V313, V323, V332, V333, theta3LU] = OffsetArticulateElbow(T6N, a2, V112, V113, V114, V133, theta2LU); % theta4, theta5, thet6: No-Flip theta4LUNF = atan2d(-V323, -V313); % deg [theta5LUNF, theta6LUNF] = OffsetArticulateWrist(V132, V133, V312, V313, V332, V333, theta4LUNF);
Solution 4: Left-Shoulder, Elbow-Up, Flip
% theta4, theta5, theta6: Flip theta4LUF = atan2d(V323, V313); % deg [theta5LUF, theta6LUF] = OffsetArticulateWrist(V132, V133, V312, V313, V332, V333, theta4LUF);
Solution 5: Right-Shoulder, Elbow-Down, No-Flip
% theta1: Right-Shoulder theta1R = atan2d(py, px) + atan2d(d3, sqrt(px*px + py*py - d3*d3)); % deg [V112, V113, V114, V132, V133, f3] = OffsetArticulateShoulder(T6N, a2, d4, theta1R); % theta2, theta3: Elbow-Down theta2RD = atan2d(pz, V114) + atan2d(-sqrt(V114*V114 + pz*pz - f3*f3), f3); % deg [V312, V313, V323, V332, V333, theta3RD] = OffsetArticulateElbow(T6N, a2, V112, V113, V114, V133, theta2RD); % theta4, theta5, thet6: No-Flip theta4RDNF = atan2d(-V323, -V313); % deg [theta5RDNF, theta6RDNF] = OffsetArticulateWrist(V132, V133, V312, V313, V332, V333, theta4RDNF);
Solution 6: Right-Shoulder, Elbow-Down, Flip
% theta4, theta5, theta6: Flip theta4RDF = atan2d(V323, V313); % deg [theta5RDF, theta6RDF] = OffsetArticulateWrist(V132, V133, V312, V313, V332, V333, theta4RDF);
Solution 7: Right-Shoulder, Elbow-Up, No-Flip
% theta2, theta3: Elbow-Up theta2RU = atan2d(pz, V114) + atan2d(sqrt(V114*V114 + pz*pz - f3*f3), f3); % deg [V312, V313, V323, V332, V333, theta3RU] = OffsetArticulateElbow(T6N, a2, V112, V113, V114, V133, theta2RU); % theta4, theta5, thet6: No-Flip theta4RUNF = atan2d(-V323, -V313); % deg [theta5RUNF, theta6RUNF] = OffsetArticulateWrist(V132, V133, V312, V313, V332, V333, theta4RUNF);
Solution 8: Right-Shoulder, Elbow-Up, Flip
% theta4, theta5, theta6: Flip theta4RUF = atan2d(V323, V313); % deg [theta5RUF, theta6RUF] = OffsetArticulateWrist(V132, V133, V312, V313, V332, V333, theta4RUF);
Eight Manipulator Configurations with the Same End-Effector Position/Orientation
ThetaSol01 = [theta1L, theta2LD, theta3LD, theta4LDNF, theta5LDNF, theta6LDNF] ThetaSol02 = [theta1L, theta2LD, theta3LD, theta4LDF, theta5LDF, theta6LDF] ThetaSol03 = [theta1L, theta2LU, theta3LU, theta4LUNF, theta5LUNF, theta6LUNF] ThetaSol04 = [theta1L, theta2LU, theta3LU, theta4LUF, theta5LUF, theta6LUF] ThetaSol05 = [theta1R, theta2RD, theta3RD, theta4RDNF, theta5RDNF, theta6RDNF] ThetaSol06 = [theta1R, theta2RD, theta3RD, theta4RDF, theta5RDF, theta6RDF] ThetaSol07 = [theta1R, theta2RU, theta3RU, theta4RUNF, theta5RUNF, theta6RUNF] ThetaSol08 = [theta1R, theta2RU, theta3RU, theta4RUF, theta5RUF, theta6RUF]
ThetaSol01 =
224.5712 180.0000 -180.0000 -44.5712 90.0000 -180.0000
ThetaSol02 =
224.5712 180.0000 -180.0000 135.4288 -90.0000 0
ThetaSol03 =
224.5712 90.0000 0 -90.0000 44.5712 -90.0000
ThetaSol04 =
224.5712 90.0000 0 90.0000 -44.5712 90.0000
ThetaSol05 =
90 0 0 90 90 -180
ThetaSol06 =
90 0 0 -90 -90 0
ThetaSol07 =
90 90 -180 90 90 -90
ThetaSol08 =
90 90 -180 -90 -90 90
Check the Solutions
OffsetArticulateFK(theta1L, theta2LD, theta3LD, theta4LDNF, theta5LDNF, theta6LDNF); OffsetArticulateFK(theta1L, theta2LD, theta3LD, theta4LDF, theta5LDF, theta6LDF); OffsetArticulateFK(theta1L, theta2LU, theta3LU, theta4LUNF, theta5LUNF, theta6LUNF); OffsetArticulateFK(theta1L, theta2LU, theta3LU, theta4LUF, theta5LUF, theta6LUF); OffsetArticulateFK(theta1R, theta2RD, theta3RD, theta4RDNF, theta5RDNF, theta6RDNF); OffsetArticulateFK(theta1R, theta2RD, theta3RD, theta4RDF, theta5RDF, theta6RDF); OffsetArticulateFK(theta1R, theta2RU, theta3RU, theta4RUNF, theta5RUNF, theta6RUNF); OffsetArticulateFK(theta1R, theta2RU, theta3RU, theta4RUF, theta5RUF, theta6RUF);
T60 =
0 0 1.0000 18.0000
0 1.0000 0 43.0000
-1.0000 0 0 43.0000
0 0 0 1.0000
T60 =
0 -0.0000 1.0000 18.0000
0 1.0000 0.0000 43.0000
-1.0000 0 0 43.0000
0 0 0 1.0000
T60 =
0 0 1.0000 18.0000
0 1.0000 0 43.0000
-1.0000 0 0 43.0000
0 0 0 1.0000
T60 =
0 0 1.0000 18.0000
0 1.0000 0 43.0000
-1.0000 0 0 43.0000
0 0 0 1.0000
T60 =
0 0 1 18
0 1 0 43
-1 0 0 43
0 0 0 1
T60 =
0 0 1 18
0 1 0 43
-1 0 0 43
0 0 0 1
T60 =
0 0 1 18
0 1 0 43
-1 0 0 43
0 0 0 1
T60 =
0 0 1 18
0 1 0 43
-1 0 0 43
0 0 0 1
This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.