Example 4.06:: Spherical Wrist: Geometric Solution (MATLAB)

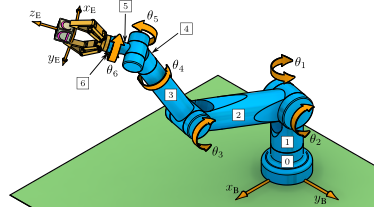
This example uses a geometric method to compute the inverse kinematics for a spherical wrist attached to the offset articulate regional structure.

Clear All Workspace Objects and Reset All Assumptions
Structural Parameters
Position and Orientation for OXYZ6
Solution for Regional Structure
Normal, Orientation, and Approach Vectors
No-Flip Solution
Flip Solution

Clear All Workspace Objects and Reset All Assumptions

clear all

Structural Parameters

a2 = 43; %cm
d3 = 18; %cm
d4 = 43; %cm

Position and Orientation for OXYZ6

Given information.

T6N = [ 0.5736  -0.8192  0.0000  18
        0.5792   0.4056  0.7071  43
       -0.5792  -0.4056  0.7071  43
        0       0        0        1 ];

Solution for Regional Structure

This solution comes from Example 4.4.

theta1 = 90; % deg
theta2 = 0; % deg
theta3 = 0; % deg
theta23 = theta2 + theta3; % deg

Normal, Orientation, and Approach Vectors

Extract these vectors from T6N.

nx = T6N(1,1);
ny = T6N(2,1);
nz = T6N(3,1);

ox = T6N(1,2);
oy = T6N(2,2);
oz = T6N(3,2);

ax = T6N(1,3);
ay = T6N(2,3);
az = T6N(3,3);

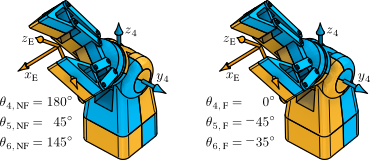
No-Flip Solution

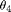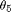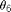Here, we solve for $\theta_{4}$ , $\theta_{5}$ , and $\theta_{6}$ using the equations for the no-flip configuration.

% Solution for theta4
A = ax*sind(theta1)*sind(theta23) - ay*cosd(theta1)*sind(theta23);
B = ax*cosd(theta23) + az*cosd(theta1)*sind(theta23);
C = -ay*cosd(theta23) - az*sind(theta1)*sind(theta23);
mag_kW_cross_a = sqrt(A*A + B*B + C*C);
sintheta4 = (ax*sind(theta1) - ay*cosd(theta1))/mag_kW_cross_a;
costheta4 = (-az*sind(theta23) - ay*sind(theta1)*cosd(theta23) ...
           - ax*cosd(theta1)*cosd(theta23))/mag_kW_cross_a;
theta4 = atan2d(sintheta4, costheta4); % deg
theta4NF = theta4 % deg

% Solution for theta5
sintheta5 = ax*(sind(theta1)*sind(theta4) - cosd(theta1)*cosd(theta23)*cosd(theta4)) ...
            - ay*(cosd(theta1)*sind(theta4) + sind(theta1)*cosd(theta23)*cosd(theta4)) ... ...
			- az*sind(theta23)*cosd(theta4);
costheta5 = -ax*cosd(theta1)*sind(theta23) - ay*sind(theta1)*sind(theta23) + az*cosd(theta23);
theta5 = atan2d(sintheta5, costheta5); % deg
theta5NF = theta5 % deg

% Solution for theta6
sintheta6 = -nx*(sind(theta1)*cosd(theta4) + cosd(theta1)*cosd(theta23)*sind(theta4)) ...
           + ny*(cosd(theta1)*cosd(theta4) - sind(theta1)*cosd(theta23)*sind(theta4)) ...
							  -nz*sind(theta23)*sind(theta4);
costheta6 = -ox*(sind(theta1)*cosd(theta4) + cosd(theta1)*cosd(theta23)*sind(theta4)) ...
			+ oy*(cosd(theta1)*cosd(theta4) - sind(theta1)*cosd(theta23)*sind(theta4)) ...
			- oz*sind(theta23)*sind(theta4);
theta6 = atan2d(sintheta6, costheta6); % deg
theta6NF = theta6 % deg

theta4NF =

   180


theta5NF =

    45


theta6NF =

  145.0005

Flip Solution

Here, we use the relations for the flip configuration.

theta4F = theta4NF - 180 % deg
theta5F = -theta5NF % deg
theta6F = theta6NF - 180 % deg

theta4F =

     0


theta5F =

   -45


theta6F =

  -34.9995

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.