Example 4.01:: RP Polar Manipulator (MATLAB)

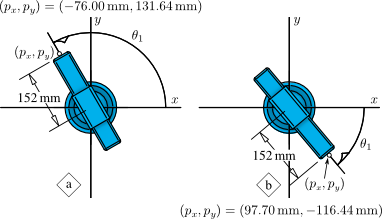
This example illustrates the importance of using the two argument inverse tangent function atan2 for computing joint angles.

Contents

Clear All Workspace Objects and Reset All Assumptions

clear all

Case (a)

px_a = -76.00; % mm
py_a = 131.64; % mm
r_a = sqrt(px_a*px_a + py_a*py_a); % mm

(i) Via the Single Argument arccosine Function

theta1_ai = acosd(px_a/r_a) % deg

theta1_ai =

  119.9992

(ii) Via the Single Argument arcsine Function

theta1_aii = asind(py_a/r_a) % deg

theta1_aii =

   60.0008

(iii) Via the Two Argument atan2 Function

theta1_aiii = atan2d(py_a, px_a) % deg

theta1_aiii =

  119.9992

(iii) Via the Single Argument atan Function

theta1_aiii_atan = atand(py_a/px_a) + 180 % deg

theta1_aiii_atan =

  119.9992

Case (b)

px_b = 97.70; % mm
py_b = -116.44; % mm
r_b = sqrt(px_b*px_b + py_b*py_b); % mm

(i) Via the Single Argument arccosine Function

theta1_bi = acosd(px_b/r_b) % deg

theta1_bi =

   50.0014

(ii) Via the Single Argument arcsine Function

theta1_bii = asind(py_b/r_b) % deg

theta1_bii =

  -50.0014

(iii) Via the Two Argument atan2 Function

theta1_biii = atan2d(py_b, px_b) % deg

theta1_biii =

  -50.0014

(iii) Via the Single Argument atan Function

theta1_biii_atan = atand(py_b/px_b) % deg

theta1_biii_atan =

  -50.0014

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.

Published with MATLAB® R2014a