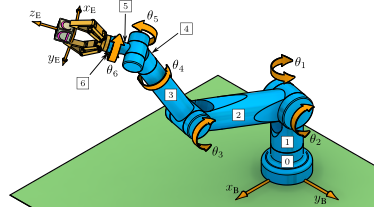
Example 3.8:: MIT Direct Drive Manipulator: Forward Kinematics (MATLAB)

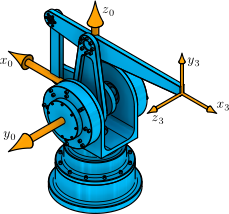
This example computes the forward kinematics for the MIT Direct Drive Manipulator, which has a four-bar sub-chain.

Clear All Workspace Objects and Reset All Assumptions
Joint Values
Structural Parameters
${\mathbf T}_{0}^{\mathrm B}$ : The Transformation from $O_{0}{\mathrm -}xyz$ to $O_{\mathrm B}{\mathrm -}xyz$
Local Transformation Variables
${\mathbf T}_{3}^{0}$ : The Transformation from $O_{3}{\mathrm -}xyz$ to $O_{0}{\mathrm -}xyz$
The Forward Kinematics as the Homogeneous Transformation ${\mathbf T}_{3}^{\mathrm B}$

Clear All Workspace Objects and Reset All Assumptions

clear all

Joint Values

theta1 = 180; % deg (motor angle)
theta2 = 90; % deg (motor angle)
phi3 = 180; % deg (motor angle)
theta3 = phi3 - theta2 - 180; % deg
theta23 = theta2 + theta3; % deg

Structural Parameters

l2 = 0.4; % m
l3 = 0.4; % m

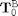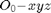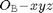
${\mathbf T}_{0}^{\mathrm B}$ : The Transformation from $O_{0}{\mathrm -}xyz$ to $O_{\mathrm B}{\mathrm -}xyz$

T0B = [1 0 0 0.00;
       0 1 0 0.00;
       0 0 1 0.56;
       0 0 0 1];

Local Transformation Variables

U214 = l2*cosd(theta2) + l3*cosd(theta23);
U224 = l2*sind(theta2) + l3*sind(theta23);

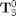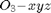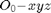
${\mathbf T}_{3}^{0}$ : The Transformation from $O_{3}{\mathrm -}xyz$ to $O_{0}{\mathrm -}xyz$

T30 = [cosd(theta1)*cosd(theta23) -cosd(theta1)*sind(theta23)  sind(theta1) U214*cosd(theta1);
       sind(theta1)*cosd(theta23) -sind(theta1)*sind(theta23) -cosd(theta1) U214*sind(theta1);
       sind(theta23)               cos(theta23)                0            U224;
       0                           0                           0            1];

The Forward Kinematics as the Homogeneous Transformation 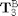${\mathbf T}_{3}^{\mathrm B}$

T3B = T0B*T30

T3B =

   -1.0000         0         0   -0.4000
         0         0    1.0000         0
         0    1.0000         0    0.9600
         0         0         0    1.0000

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.