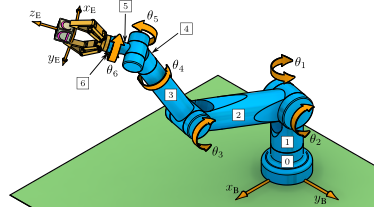
Robot Mechanics and Control Robot Mechanics and Control

Example 6.9: Offset Spherical Manipulator: Joint Torques/Forces (MATLAB)

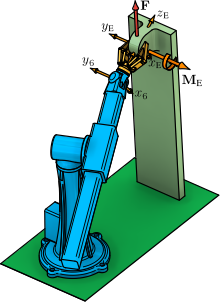
Offset Spherical Manipulator: Joint Torques/Forces

This example illustrates a computation for the joint torques/forces when the offset spherical manipulator applies a wrench on its environment.

Contents

Clear All Workspace Objects and Reset All Assumptions

clear all

Given Wrench 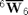$^{6}\overline{\mathbf W}_{6}$

 W6Res6 = [-8.090; 0; 5.878; 0; -207.983; 0]; % [force (N); moment (N-cm)]

Structural Parameters

d2 = 18; % cm

Joint Values

theta1 = 112.71; % deg
theta2 = -61.01; % deg
d3 = 47.13; % cm
theta4 = 64.52; % deg
theta5 = 20.30; % deg
theta6 = -76.82; % deg

Local Variables

U511 = cosd(theta5)*cosd(theta6);
U512 = -cosd(theta5)*sind(theta6);
U521 = sind(theta5)*cosd(theta6);
U522 = -sind(theta5)*sind(theta6);
U411 = U511*cosd(theta4) - sind(theta4)*sind(theta6);
U412 = U512*cosd(theta4) - sind(theta4)*cosd(theta6);
U413 = -cosd(theta4)*sind(theta5);
U421 = U511*sind(theta4) + cosd(theta4)*sind(theta6);
U422 = U512*sind(theta4) + cosd(theta4)*cosd(theta6);
U423 = -sind(theta4)*sind(theta5);
U211 = U411*cosd(theta2) - U521*sind(theta2);
U212 = U412*cosd(theta2) - U522*sind(theta2);
U213 = U413*cosd(theta2) - sind(theta2)*cosd(theta5);
U214 = -d3*sind(theta2);
U221 = U411*sind(theta2) + U521*cosd(theta2);
U222 = U412*sind(theta2) + U522*cosd(theta2);
U223 = U413*sind(theta2) + cosd(theta2)*cosd(theta5);

The manipulator Jacobian 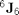$^{6}{\mathbf J}_{6}$

J6Res6(:,1) = [U221; U222; U223; d2*U211+U214*U421; d2*U212+U214*U422; d2*U213+U214*U423];
J6Res6(:,2) = [-U421; -U422; -U423; -d3*U411; -d3*U412; -d3*U413];
J6Res6(:,3) = [0; 0; 0; U521; U522; cosd(theta5)];
J6Res6(:,4) = [U521; U522; cosd(theta5); 0; 0; 0];
J6Res6(:,5) = [-sind(theta6); -cosd(theta6); 0; 0; 0; 0];
J6Res6(:,6) = [0; 0; 1; 0; 0; 0];

J6Res6

J6Res6 =

   -0.8110    0.2258         0    0.0791    0.9737         0
    0.0001   -0.9225         0    0.3378   -0.2280         0
    0.5851    0.3132         0    0.9379         0    1.0000
    0.4067  -45.7610    0.0791         0         0         0
   44.9779   -8.8140    0.3378         0         0         0
    0.5535    7.0342    0.9379         0         0         0

Form the Ray to Axis Coordinate Transfer Matrix ${\mathbf \Pi}$

PI = [zeros(3) eye(3);
      eye(3)   zeros(3)];

Joint Torques/Forces 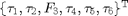$\{ \tau_{1}, \tau_{2}, F_{3}, \tau_{4}, \tau_{5}, \tau_{6} \}^{\mathrm T}$

Tau = transpose(J6Res6)*PI*W6Res6 % [ N-cm; N-cm; N; N-cm; N-cm; N-cm]

Tau =

   -0.0649
  603.4080
    4.8730
  -70.2560
   47.4224
         0

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for other relevant files.


Published with MATLAB® R2014a