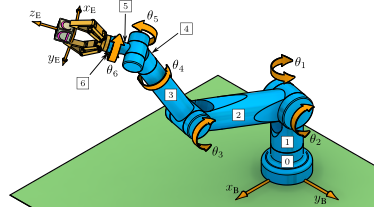
Robot Mechanics and Control Robot Mechanics and Control

Extra Example:: Puma 560 Manipulator: Jacobian Computation (MATLAB)

This example illustrates a computation with specific joint values for the Puma 560 Jacobian.

Contents

Joint Values

theta1 = 90; % deg
theta2 = 90; % deg
theta3 = -180; % deg
theta23 = theta2 + theta3; % deg
theta4 = 90; % deg
theta5 = 90; % deg
theta6 = -90; % deg

Structural Parameters

a2 = 43.18; % cm
a3 = 1.91; % cm
d3 = 12.54; % cm
d4 = 43.18; % cm

Local Variables From U-Matrices

U511 = cosd(theta5)*cosd(theta6);
U512 = -cosd(theta5)*sind(theta6);
U521 = sind(theta5)*cosd(theta6);
U522 = -sind(theta5)*sind(theta6);

U411 = -sind(theta4)*sind(theta6) + U511*cosd(theta4);
U412 = -sind(theta4)*cosd(theta6) + U512*cosd(theta4);
U413 = -cosd(theta4)*sind(theta5);
U421 = cosd(theta4)*sind(theta6) + U511*sind(theta4);
U422 = cosd(theta4)*cosd(theta6) + U512*sind(theta4);
U423 = -sind(theta4)*sind(theta5);

U311 = U411*cosd(theta3) - U521*sind(theta3);
U312 = U412*cosd(theta3) - U522*sind(theta3);
U313 = -sind(theta3)*cosd(theta5) + U413*cosd(theta3);
U314 = -d4*sind(theta3) + a3*cosd(theta3);
U321 = U411*sind(theta3) + U521*cosd(theta3);
U322 = U412*sind(theta3) + U522*cosd(theta3);
U323 = cosd(theta3)*cosd(theta5) + U413*sind(theta3);
U324 = a3*sind(theta3) + d4*cosd(theta3);

U211 = U411*cosd(theta23) - U521*sind(theta23);
U212 = U412*cosd(theta23) - U522*sind(theta23);
U213 = -sind(theta23)*cosd(theta5) + U413*cosd(theta23);
U214 = a2* cosd(theta2) - d4*sind(theta23) + a3*cosd(theta23);
U221 = U411*sind(theta23) + U521*cosd(theta23);
U222 = U412*sind(theta23) + U522*cosd(theta23);
U223 = cosd(theta23)*cosd(theta5) + U413*sind(theta23);
U224 = a2*sind(theta2) + a3*sind(theta23) + d4*cosd(theta23);

Joint-Screw 1: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{1|6}$

Jacobian(:,1) = [U221; U222; U223; d3*U211 + U214*U421; d3*U212 + U214*U422; d3*U213 + U214*U423];

Joint-Screw 2: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{2|6}$

Jacobian(:,2) = [-U421; -U422; -U423; U214*U221 - U211*U224; U214*U222 - U212*U224; U214*U223 - U213*U224];

Joint-Screw 3: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{3|6}$

Jacobian(:,3) = [-U421; -U422; -U423; U314*U321 - U311*U324; U314*U322 - U312*U324; U314*U323 - U313*U324];

Joint-Screw 4: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{4|6}$

Jacobian(:,4) = [U521; U522; cosd(theta5); 0; 0; 0];

Joint-Screw 5: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{5|6}$

Jacobian(:,5) = [-sind(theta6); -cosd(theta6); 0; 0; 0; 0];

Joint-Screw 6: $^{6}\hspace{0.34em}\rule[-0.17em]{0.01in}{1.0em}\hspace{-0.34em}{\mathbf S}_{6|6}$

Jacobian(:,6) = [0; 0; 1; 0; 0; 0];

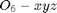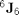
The Jacobian Resolved in $O_{6}-xyz$: $^{6}\mathbf{J}_{6}$

J6Res6 = Jacobian

J6Res6 =

   -1.0000         0         0         0    1.0000         0
         0         0         0    1.0000         0         0
         0    1.0000    1.0000         0         0    1.0000
         0  -43.1800  -43.1800         0         0         0
   12.5400  -41.2700    1.9100         0         0         0
  -43.1800         0         0         0         0         0

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.


Published with MATLAB® R2014a