Robot Mechanics and Control Robot Mechanics and Control

Example 4.04:: OAM Regional: Geometric Solution (MATLAB)

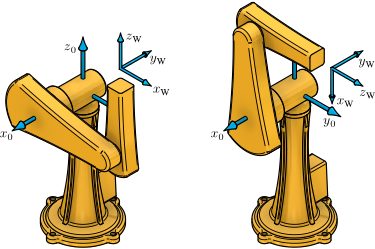
Offset Articulate Regional Structure

This example computes the inverse kinematics for the offset articulate regional structure via a geometric solution.

Contents

Clear All Workspace Objects and Reset All Assumptions

clear all

Structural Parameters

a2 = 43; % cm
d3 = 18; % cm
d4 = 43; % cm

Position for the Wrist Center Origin 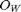$O_{W}$

px = 18; % cm
py = 43; % cm
pz = 43; % cm

Geometric Equations

r2 = sqrt(px*px + py*py + pz*pz - d3*d3); % cm
cos_phi2 = (a2*a2 + r2*r2 - d4*d4)/(2*a2*r2);
cos_phi3 = (a2*a2 + d4*d4 - r2*r2)/(2*a2*d4);
sin_phi2 = sqrt(1 - cos_phi2*cos_phi2);
sin_phi3 = sqrt(1 - cos_phi3*cos_phi3);
phi2 = atan2d(sin_phi2, cos_phi2); % deg
phi3 = atan2d(sin_phi3, cos_phi3); % deg

Right-Shoulder Solution for 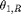$\theta_{1,R}$

theta1R = atan2d(py, px) + atan2d(d3, sqrt(px*px + py*py - d3*d3)) % deg

theta1R =

    90

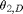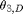
Elbow-Down Solution for $\theta_{2,D}$ and $\theta_{3,D}$

theta2D = atan2d(pz, sqrt(px*px + py*py - d3*d3)) - phi2 % deg
theta3D = 90 - phi3 % deg

theta2D =

     0


theta3D =

     0

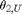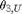
Elbow-Up Solution for $\theta_{2,U}$ and $\theta_{3,U}$

theta2U = atan2d(pz, sqrt(px*px + py*py - d3*d3)) + phi2 % deg
theta3U = phi3 - 270 % deg

theta2U =

    90


theta3U =

  -180

This MATLAB example illustrates a computation from the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015. See http://www.RobotMechanicsControl.info for additional relevant files.


Published with MATLAB® R2014a