
|
|
|
|
|
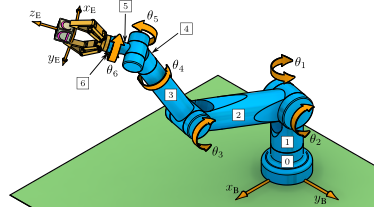
Example 3.3:: Determining an A-Matrix (Mathematica)
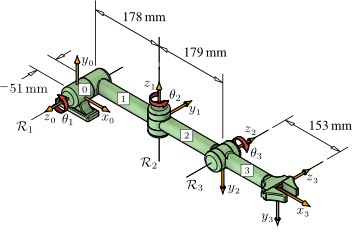
This example formulates the A-matrices for a 3R spatial manipulator.
Contents
Define a Generic A-Matrix Function
A[θ_, d_, a_, α_] := {{Cos[θ], -Cos[α] Sin[θ], Sin[α] Sin[θ], a Cos[θ]}, {Sin[θ], Cos[α] Cos[θ], -Cos[θ] Sin[α], a Sin[θ]}, {0, Sin[α], Cos[α], d}, {0, 0, 0, 1}};
DH Parameters
θ1=.; d1=-51; a1=178; α1=-90 Degree; θ2=.; d2=0; a2=179; α2=-90 Degree; θ3=.; d3=0; a3=153; α3=0 Degree;
A10: Transformation from the Link 1 Frame to the Link 0 Frame
A10 = A[θ1, d1, a1, α1];
MatrixForm[A10]
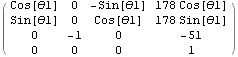
A21: Transformation from the Link 2 Frame to the Link 1 Frame
A21 = A[θ2, d2, a2, α2];
MatrixForm[A21]
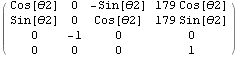
A32: Transformation from the Link 3 Frame to the Link 2 Frame
A32 = A[θ3, d3, a3, α3];
MatrixForm[A32]
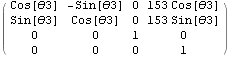
This Mathematica file resides at http://www.RobotMechanicsControl.info. For a complete description of this example, along with the requisite background, definitions, and notation, see the textbook Fundamentals of Robot Mechanics by G. L. Long, Quintus-Hyperion Press, 2015.